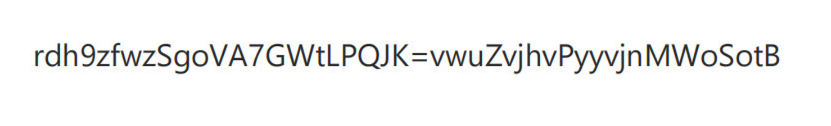第一周题目不难，所有方向都可以借助搜索引擎和AI解决，第一周所有方向全解。第二周精力有限，主要写了Misc、Crypto和逆向，pwn和web写了一半左右。

两周题目看来，我认为Misc题目相对其他题目来说难度跨度比较大，有些题目运用的知识还是比较全面的。

现在第三周正在进行中，Misc也是引入了新内容区块链和内存取证，密码引入了Coppersmith。尽管是新生赛，还是颇有趣味，尤其是Misc的流量分析这块，确实很有想法。

Week1

Misc

我不要革命失败

附件用windbg打开，等待加载完毕后，执行analyze -v命令，然后得到的数据给ai分析，最终得到flag

flag{CRITICAL_PROCESS_DIED_svchost.exe}

MISC城邦-压缩术

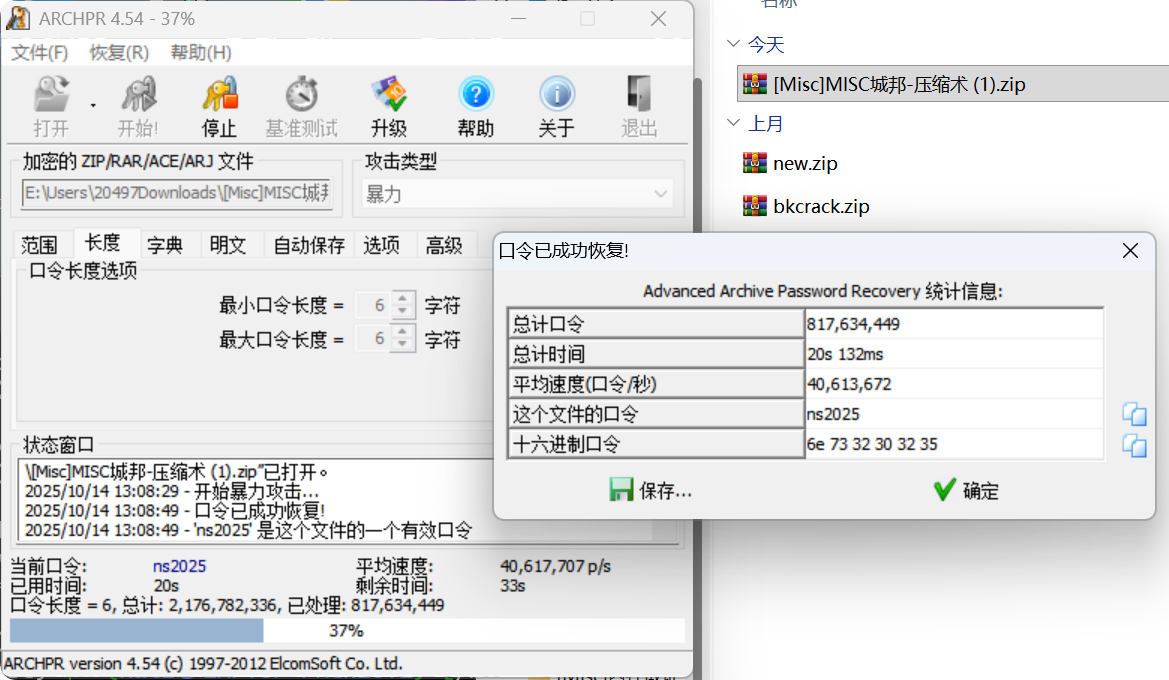
题目描述：欢迎挑战者们来到压缩术的考验关卡，本关考察压缩术的综合使用，请挑战者们通过6位密码门开始挑战吧！(要想使用压缩术，请先念咒语“abcd…xyz0123…789”)

可知密码为6位的数字加小写字母

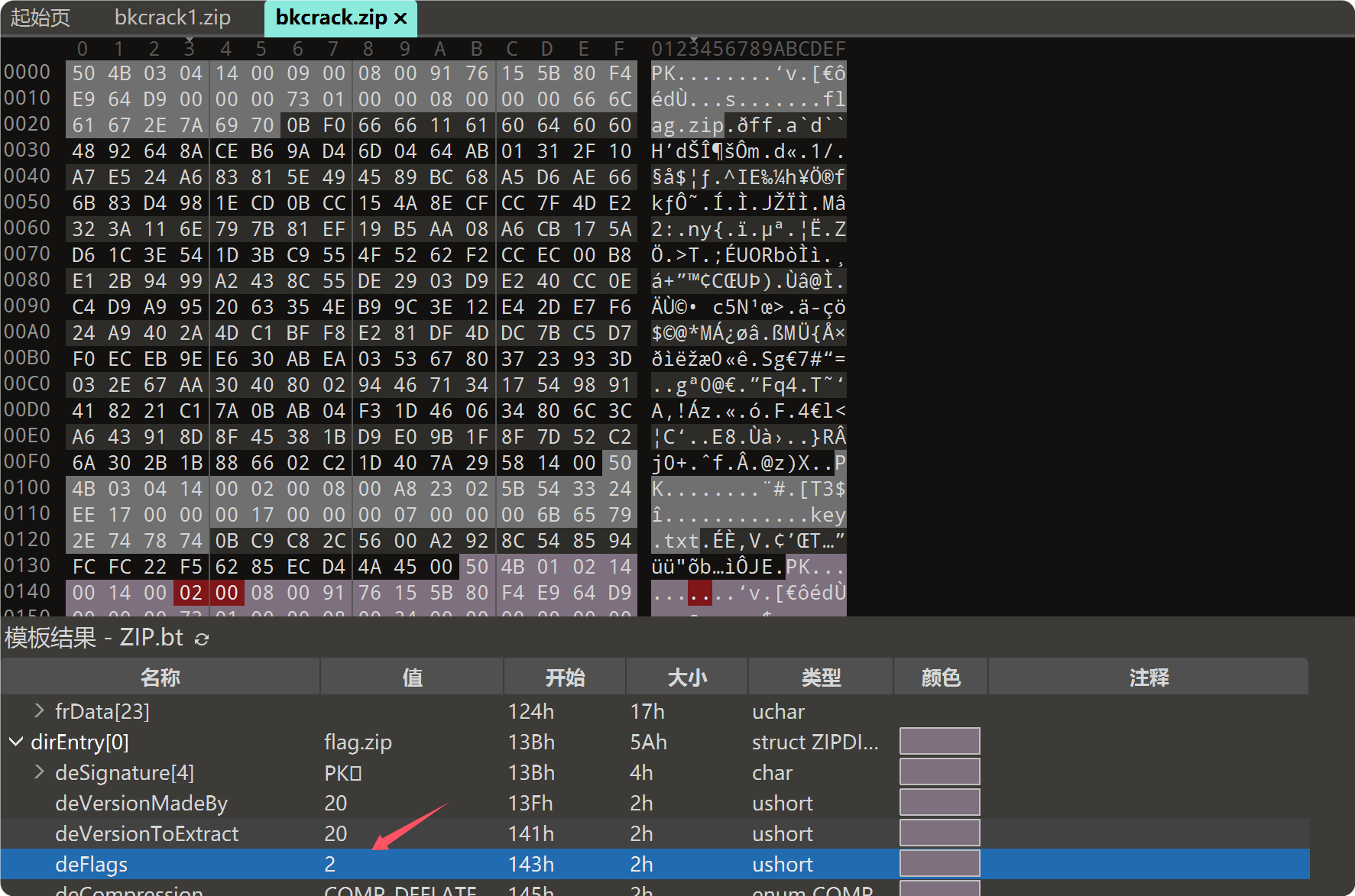
第二阶段是伪加密

写个对应字段为偶数即可

最后是明文攻击

1 2	bkcrack -C flag.zip -c key.txt -p key.txt -o 0 bkcrack -C flag.zip -c key.txt -k xxx -U new.zip 123

最后解压得到flag

flag{You_have_mastered_the_zip_magic!}

EZ_fence

题目描述：rar发现一张残缺的照片竟然需要4颗钉子才能钉住，照片里面似乎藏着秘密。

附件为一张jpg图片后面有多余数据，用工具分解

binwalk fence1.1.jpg

DECIMAL       HEXADECIMAL     DESCRIPTION
--------------------------------------------------------------------------------
0             0x0             JPEG image data, JFIF standard 1.01
53556         0xD134          RAR archive data, version 5.x
foremost fence1.1.jpg

得到rar，但需要输入密码

我们可以看到题目附件图片

fence分4栏解密得到

1	rSvMwgdouWZVhAvoj79GhSvWztPoyLfPytvQwJjBnKz=

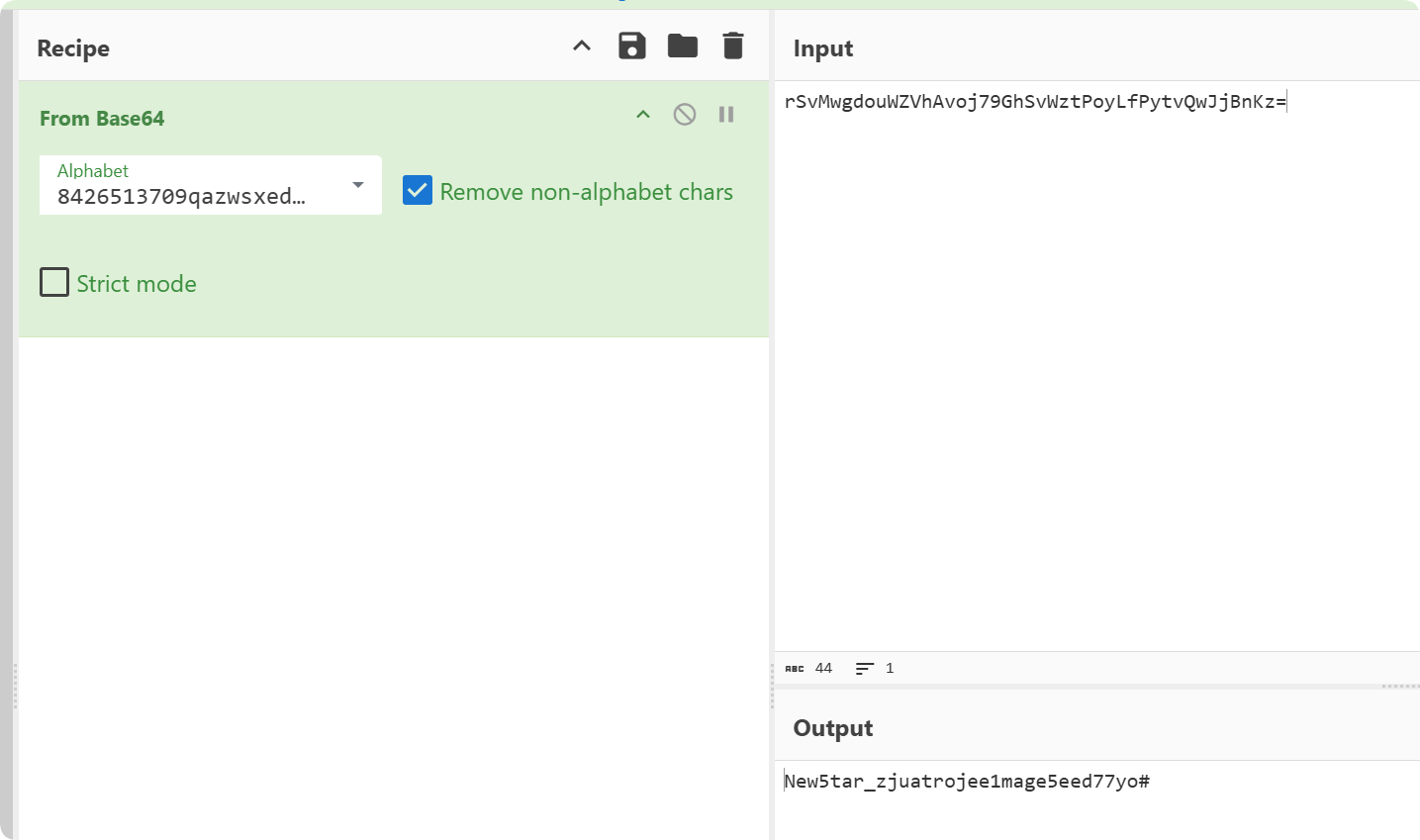
直接base64解码不行，我们修改jpg高度得到码表

1	8426513709qazwsxedcrfvtgbyhnujmikop1QWSAERFDTYHGUIKJOPLMNBVCXZ+\

得到rar密码：New5tar_zjuatrojee1mage5eed77yo#

解压得到flag

flag{y0u_kn0w_ez_fence_tuzh0ng}

前有文字，所以搜索很有用

有三部分

第一部分零宽隐写得到：ZmxhZ3t5b3Vf

第二部分brainfuck编码

得到key：brainfuckisgooooood

here's key
+++++ ++++[ ->+++ +++++ +<]>+ +++++ +++++ +++++ +.<++ ++[-> ++++< ]>.<+
+++[- >---- <]>-. +++++ +++.+ ++++. ----- ---.< +++[- >+++< ]>+++ +++.<
++++[ ->--- -<]>- -.+++ +++++ .--.< +++[- >+++< ]>+.< +++[- >---< ]>---
.++++ ++++. ..... <+++[ ->--- <]>-- .<

这里还有snow隐写，将咏雪.docx里的所有字符复制到txt，然后解snow隐写

1	snow -p "brainfuckisgooooood" 1.txt ret.txt

得到第二部分—– …- …– .-. -.-. ….- – . ..–.-

第三部分为字频分析，

得到cH@1LenG3s}

然后将第一段base64解码，第二段morse解码与第三段拼接得到flag

flag{you_0V3RC4ME_cH@1LenG3s}

OSINT-天空belong

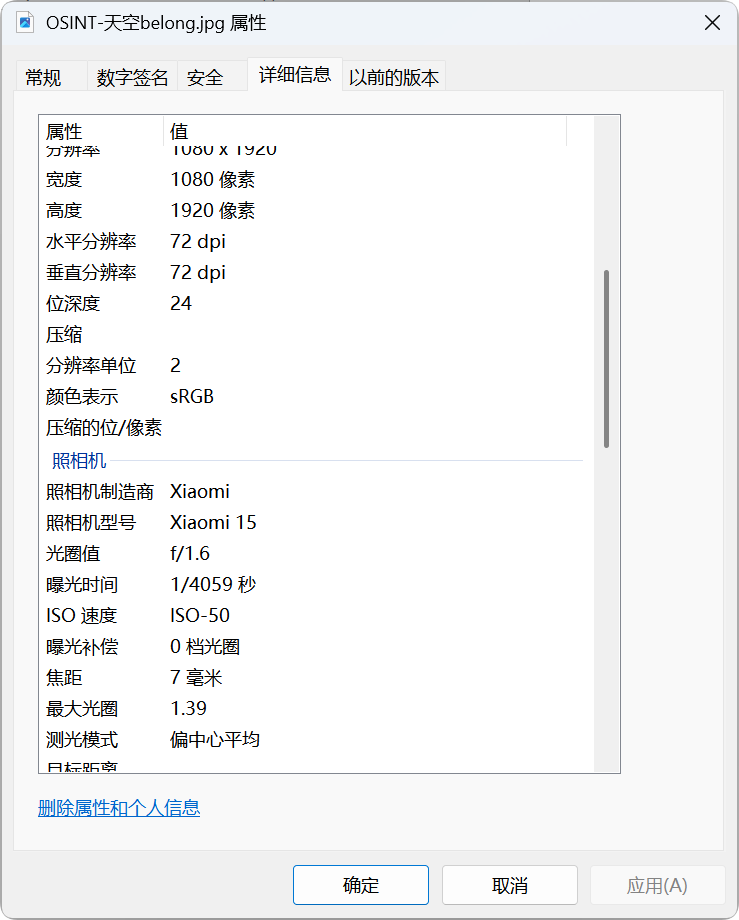
图寻题，去年也有这种注册机号的题，不过今年难度低一些，我们可以根据图片拍摄时间，以及拍摄的机翼上的注册机号搜索，最后可追踪到航线

flag格式：flag{航班号_当前已经经过的省会城市名称(**市)_所拍摄设备制造商}

flag{UQ3574_武汉市_Xiaomi}

flag{Welcome_to_NewStar_CTF_2025!}

Crypto

唯一表示

题目：

from sympy.ntheory.modular import crt
from Crypto.Util.number import bytes_to_long
from sympy import primerange
import uuid

# 生成素数列表
primes = list(primerange(2, 114514))

# 生成随机 flag，并转换为整数
flag = "flag{" + str(uuid.uuid4()) + "}"
message_int = bytes_to_long(flag.encode())

def fun(n: int):
    """
    给定整数 n，返回它对若干个素数模的余数列表，
    直到用这些余数和模数 CRT 重建出的值恰好等于 n。
    """
    used_primes = [2]          # 当前使用的素数列表，先用 2 开始
    prime_index = 1            # primes[0] 已用，从 primes[1] 开始
    while True:
        # 计算 n 对当前所有模数的余数
        remainders = [n % p for p in used_primes]

        # 用 CRT 尝试重建 n
        reconstructed, _ = crt(used_primes, remainders)

        # 如果重建成功，返回余数列表
        if reconstructed == n:
            return remainders

        # 否则继续添加新的素数，扩大模数集合
        used_primes.append(primes[prime_index])
        prime_index += 1

# 计算 message_int 的余数表示
c = fun(message_int)

print(c)


"""
[1, 2, 2, 4, 0, 2, 11, 11, 8, 23, 1, 30, 35, 0, 18, 30, 55, 60, 29, 42, 8, 13, 49, 11, 69, 26, 8, 73, 84, 67, 100, 9, 77, 72, 127, 49, 57, 74, 70, 129, 146, 45, 35, 180, 196, 101, 100, 146, 100, 194, 2, 161, 35, 155]
"""

题解：

已知：余数列表和对应的模数列表

直接调用CRT就能得到原始整数

from sympy.ntheory.modular import crt
from Crypto.Util.number import long_to_bytes
from sympy import primerange

def solve():
    """
    根据给定的余数列表 c 和原始程序的逻辑，恢复 flag。
    """
    # 这是题目给出的余数列表
    c = [1, 2, 2, 4, 0, 2, 11, 11, 8, 23, 1, 30, 35, 0, 18, 30, 55, 60, 29, 42, 8, 13, 49, 11, 69, 26, 8, 73, 84, 67, 100, 9, 77, 72, 127, 49, 57, 74, 70, 129, 146, 45, 35, 180, 196, 101, 100, 146, 100, 194, 2, 161, 35, 155]

    # 1. 生成和原程序完全一样的素数列表
    primes = list(primerange(2, 114514))

    # 2. 根据 c 的长度，确定用作模数的素数列表
    num_primes_used = len(c)
    moduli = primes[:num_primes_used]

    # 3. 使用中国剩余定理恢复原始的整数
    # crt 函数需要两个列表：模数列表和对应的余数列表
    reconstructed_int, _ = crt(moduli, c)

    # 4. 将恢复的整数转换回字节，然后解码为字符串
    flag_bytes = long_to_bytes(reconstructed_int)
    flag = flag_bytes.decode('utf-8')

    return flag

# 运行解题程序并打印结果
recovered_flag = solve()
print("恢复的 flag 是:")
print(recovered_flag)

小跳蛙

题目

banner = """
Welcome to Cathylin's cryptography learning platform, where we learn an algorithm through an interesting problem.

There is a frog on the grid point (a, b). When a > b, it will jump to (a-b, b); when a < b, it will jump to (a, b-a); and when a = b, it will stay where it is.

Next, I will provide five sets of (a, b), and please submit the final position (x, y) of the frog in sequence

If you succeed, I will give you a mysterious flag.
"""
print(banner)

import re
import random
from secret import flag


cnt = 0
while cnt < 5:
    a = random.randint(1, 10**(cnt+1))
    b = random.randint(1, 10**(cnt+1))
    print(  str(cnt+1) + ".(a,b) is: (" + str(a) + "," + str(b) + ")")
    user_input = input("Please input the final position of the frog (x,y) :")
    pattern = r'[()]?(\d+)[,\s]+(\d+)[)]?'
    match = re.match(pattern, user_input.strip())
    if match:
        x, y = map(int, match.groups())
    else:
        print("Unable to parse the input. Please check the format and re-enter")
        continue

    original_a, original_b = a, b
    while a != b:
        if a > b:
            a = a - b
        else:
            b = b - a

    if x == a and y == b:
        print("Congratulations, you answered correctly! Keep going for " + str(4-cnt) + " more times and you will get the mysterious flag!")
        cnt += 1
    else:
        print("Unfortunately, you answered incorrectly. The correct answer is({}, {}). Please start learning again".format(a, b))
        break

if cnt == 5:
    print("Congratulations, you answered all the questions correctly!")
    print("Mysterious Flag:" + flag)

题解：

代码中说的以及很清楚了

There is a frog on the grid point (a, b). When a > b, it will jump to (a-b, b); when a < b, it will jump to (a, b-a); and when a = b, it will stay where it is.

Next, I will provide five sets of (a, b), and please submit the final position (x, y) of the frog in sequence

If you succeed, I will give you a mysterious flag.

import re
import math
from pwn import *

# 设置目标主机和端口
HOST = '39.106.48.123'
PORT = 13049

# 连接到目标服务
# context.log_level = 'debug' # 取消此行注释可查看详细的底层交互数据
try:
    r = remote(HOST, PORT)

    # 循环5次，应对5轮挑战
    for i in range(5):
        # 接收数据，直到接收到输入提示符为止。
        # 这是最稳健的方法，可以一次性接收完欢迎语、上一轮的结果和新一轮的题目。
        output = r.recvuntil(b'Please input the final position of the frog (x,y) :').decode()

        # 打印从服务器接收到的原始信息，方便调试
        print(f"--- Round {i+1} Received ---")
        print(output)
        print("------------------------")

        # 使用正则表达式从接收到的一大块文本中找到最后一组 (a,b)
        # 这确保我们总是在解当前这道题
        matches = re.findall(r'\((\d+),(\d+)\)', output)
        if not matches:
            print("错误：无法从服务器输出中解析出 (a, b)。")
            break

        # 最后一组匹配项就是当前的题目
        a_str, b_str = matches[-1]
        a = int(a_str)
        b = int(b_str)
        print(f"解析到题目: (a, b) = ({a}, {b})")

        # 使用 math.gcd() 高效计算最大公约数
        g = math.gcd(a, b)
        
        # 构造答案 "(g,g)"
        answer = f"({g},{g})"
        print(f"计算出最大公约数: {g}. 发送答案: {answer}\n")

        # 发送答案
        r.sendline(answer.encode())

    # 循环结束后，接收最后的所有输出，其中包含 flag
    final_output = r.recvall(timeout=2).decode()
    print("--- Final Output (Flag) ---")
    print(final_output)
    print("---------------------------")

except Exception as e:
    print(f"程序执行出错: {e}")

finally:
    # 关闭连接
    if 'r' in locals() and r:
        r.close()

flag{Go0d_j0b_t0_Cl34r_thi5_Diff3r3nt_t45k_4_u}

初识RSA

题目

from Crypto.Util.number import *
import hashlib
from gmpy2 import *
key=b'??????'
assert len(key)==6 
KEY = hashlib.md5(key).hexdigest().encode()
print('KEY=',KEY)

flag=b'flag{?????????????}'

m=bytes_to_long(flag)

e=65537
p=getPrime(512)
q=getPrime(512)
n=pow(p,3)* pow(q,2)
c=pow(m,e,n)

P=p^(bytes_to_long(key))

print("P=",P)
print("n=",n)
print("c=",c)

'''
KEY = b'5ae9b7f211e23aac3df5f2b8f3b8eada' 
P= 8950704257708450266553505566662195919814660677796969745141332884563215887576312397012443714881729945084204600427983533462340628158820681332200645787691506
n= 44446616188218819786207128669544260200786245231084315865332960254466674511396013452706960167237712984131574242297631824608996400521594802041774252109118569706894250996931000927100268277762882754652796291883967540656284636140320080424646971672065901724016868601110447608443973020392152580956168514740954659431174557221037876268055284535861917524270777789465109449562493757855709667594266126482042307573551713967456278514060120085808631486752297737122542989222157016105822237703651230721732928806660755347805734140734412060262304703945060273095463889784812104712104670060859740991896998661852639384506489736605859678660859641869193937584995837021541846286340552602342167842171089327681673432201518271389316638905030292484631032669474635442148203414558029464840768382970333
c= 42481263623445394280231262620086584153533063717448365833463226221868120488285951050193025217363839722803025158955005926008972866584222969940058732766011030882489151801438753030989861560817833544742490630377584951708209970467576914455924941590147893518967800282895563353672016111485919944929116082425633214088603366618022110688943219824625736102047862782981661923567377952054731667935736545461204871636455479900964960932386422126739648242748169170002728992333044486415920542098358305720024908051943748019208098026882781236570466259348897847759538822450491169806820787193008018522291685488876743242619977085369161240842263956004215038707275256809199564441801377497312252051117441861760886176100719291068180295195677144938101948329274751595514805340601788344134469750781845
'''

题解：

关键是要知道key，我们已知key为6字节和他的md5值，可以直接用在线网站查如cmd5或者爆破，得到crypto

然后异或恢复p，然后根据n恢复q，最后计算欧拉函数，然后就是常规rsa了

from Crypto.Util.number import *
from gmpy2 import *
P= 8950704257708450266553505566662195919814660677796969745141332884563215887576312397012443714881729945084204600427983533462340628158820681332200645787691506
n= 44446616188218819786207128669544260200786245231084315865332960254466674511396013452706960167237712984131574242297631824608996400521594802041774252109118569706894250996931000927100268277762882754652796291883967540656284636140320080424646971672065901724016868601110447608443973020392152580956168514740954659431174557221037876268055284535861917524270777789465109449562493757855709667594266126482042307573551713967456278514060120085808631486752297737122542989222157016105822237703651230721732928806660755347805734140734412060262304703945060273095463889784812104712104670060859740991896998661852639384506489736605859678660859641869193937584995837021541846286340552602342167842171089327681673432201518271389316638905030292484631032669474635442148203414558029464840768382970333
c= 42481263623445394280231262620086584153533063717448365833463226221868120488285951050193025217363839722803025158955005926008972866584222969940058732766011030882489151801438753030989861560817833544742490630377584951708209970467576914455924941590147893518967800282895563353672016111485919944929116082425633214088603366618022110688943219824625736102047862782981661923567377952054731667935736545461204871636455479900964960932386422126739648242748169170002728992333044486415920542098358305720024908051943748019208098026882781236570466259348897847759538822450491169806820787193008018522291685488876743242619977085369161240842263956004215038707275256809199564441801377497312252051117441861760886176100719291068180295195677144938101948329274751595514805340601788344134469750781845
key = b'crypto'
e=65537
p = P^bytes_to_long(key)
q = iroot(n//(p**3),2)[0]
phi =  p**2*(p-1)*q*(q-1)
d = inverse(e,phi)
print(long_to_bytes(pow(c,d,n)))

flag{W3lc0me_t0_4h3_w0rl4_0f_Cryptoooo!}

随机数之旅1

题目：

import uuid
from Crypto.Util.number import getPrime, bytes_to_long
import random

# 生成随机 flag 并转换为整数
flag = "flag{" + str(uuid.uuid4()) + "}"
message_int = bytes_to_long(flag.encode())

# 生成两个素数：
# p 的比特长度比 message_int 略大
# a 的比特长度和 p 相同
p = getPrime(message_int.bit_length() + 3)
a = getPrime(p.bit_length())

print(f"a = {a}")
print(f"p = {p}")

# hint 序列：以随机数为起点，按递推关系生成 5 次
# hint[i+1] = (a * hint[i] + message_int) mod p
hint_values = [random.randint(1, p - 1)]

for _ in range(5):
    next_value = (a * hint_values[-1] + message_int) % p
    hint_values.append(next_value)

print("hint =", hint_values)

"""
a = 295789025762601408173828135835543120874436321839537374211067344874253837225114998888279895650663245853
p = 516429062949786265253932153679325182722096129240841519231893318711291039781759818315309383807387756431
hint = [184903644789477348923205958932800932778350668414212847594553173870661019334816268921010695722276438808, 289189387531555679675902459817169546843094450548753333994152067745494929208355954578346190342131249104, 511308006207171169525638257022520734897714346965062712839542056097960669854911764257355038593653419751, 166071289874864336172698289575695453201748407996626084705840173384834203981438122602851131719180238215, 147110858646297801442262599376129381380715215676113653296571296956264538908861108990498641428275853815, 414834276462759739846090124494902935141631458647045274550722758670850152829207904420646985446140292244]

"""

题解：

LCG密码，这里主要考查的是由hint[i+1] = (a * hint[i] + message_int) mod p解出message_int，因为a,phint已知我们选取两个hint便可以构造方程message_int = (h1 - a * h0) % p解出了

from Crypto.Util.number import long_to_bytes
a = 295789025762601408173828135835543120874436321839537374211067344874253837225114998888279895650663245853
p = 516429062949786265253932153679325182722096129240841519231893318711291039781759818315309383807387756431
hint = [184903644789477348923205958932800932778350668414212847594553173870661019334816268921010695722276438808, 289189387531555679675902459817169546843094450548753333994152067745494929208355954578346190342131249104, 511308006207171169525638257022520734897714346965062712839542056097960669854911764257355038593653419751, 166071289874864336172698289575695453201748407996626084705840173384834203981438122602851131719180238215, 147110858646297801442262599376129381380715215676113653296571296956264538908861108990498641428275853815, 414834276462759739846090124494902935141631458647045274550722758670850152829207904420646985446140292244]
h0 = hint[0]
h1 = hint[1]
message_int = (h1 - a * h0) % p
flag = long_to_bytes(message_int)
print(flag)

flag{c3bc3ead-01e3-491b-aa2d-d2f042449fd6}

Sagemath使用指哪？

1
2
3

(sage) ┌──(kali㉿LAPTOP-PKCNLOTE)-[/mnt/e/Users/20497Downloads/[Cry]Sagemath使用指哪？]
└─$ sage sagematch.sage
flag{e142d08c-7e7d-43ed-b5ad-af51ffc512ee}

flag{e142d08c-7e7d-43ed-b5ad-af51ffc512ee}

Week2

Misc

星期四的狂想

流量分析，导出http协议最大的文件有

--------------------------fede7f03cb0fbf04
Content-Disposition: form-data; name="file"; filename="crazy.php"
Content-Type: application/octet-stream

<?php
echo "Hello, world!";

$flag = base64_encode(file_get_contents("/flag"));
$hahahahahaha = '';
foreach (str_split($flag, 10) as $part) {
  if (rand(0, 1)) {
    $part = strrev($part);
  } else {
    $part = str_rot13($part);
  }
  $hahahahahaha .= $part;
}

$_GLOBALS['ThURSDAY'] = $hahahahahaha;
function code($x) {
  return "Cookie: token=" . base64_encode($x);
}

?>
--------------------------fede7f03cb0fbf04--

大概意思是将flag内容base64加密后每10字符一组反转然后Rot13变换，写入$hahahahahaha变量

1	$getFunction("vivo")(code($GLOBALS[$_GET['cmd']]));

流量中还记录了上传了些其他文件，如上面的，我们继续追踪得到下面

POST /uploads/?cmd=ThURSDAY HTTP/1.1
Host: 172.17.0.2
User-Agent: curl/7.58.0
Accept: */*
Content-Length: 14
Content-Type: application/x-www-form-urlencoded

file=crazy.php
HTTP/1.1 200 OK
Date: Fri, 19 Sep 2025 00:24:48 GMT
Server: Apache/2.4.29 (Ubuntu)
Cookie: token=R2FYdDNaaHhtWlMwS21TR0szRVZxSUF4QVV5c0hLVzlWZXN0MllwVmdDOUJUTlBaVlM9PQ==
Content-Length: 18
Content-Type: text/html; charset=UTF-8

***n
Hello, world!

可看到该流量，通过?cmd=ThURSDAY来获取$hahahahahaha即Cookie: token=R2FYdDNaaHhtWlMwS21TR0szRVZxSUF4QVV5c0hLVzlWZXN0MllwVmdDOUJUTlBaVlM9PQ==

接着可以写出解题程序

token_str = "R2FYdDNaaHhtWlMwS21TR0szRVZxSUF4QVV5c0hLVzlWZXN0MllwVmdDOUJUTlBaVlM9PQ=="

import base64, codecs, re, itertools

# 解码 token -> 得到被变换后的字符串
trans = base64.b64decode(token_str).decode()

# 按 PHP 的 str_split(...,10) 切分
chunks = [ trans[i:i+10] for i in range(0, len(trans), 10) ]

def undo_rot13(s): return codecs.decode(s, 'rot_13')

# 穷举每个块的两种逆向操作：reverse 或 rot13（注意 rot13 的逆就是再 rot13）
n = len(chunks)
for mask in range(1<<n):
    parts = []
    for i, c in enumerate(chunks):
        if (mask >> i) & 1:
            parts.append(c[::-1])       # 如果原来是 reverse，解法是再 reverse
        else:
            parts.append(undo_rot13(c)) # 如果原来是 rot13，解法是再 rot13
    candidate = "".join(parts)
    try:
        decoded = base64.b64decode(candidate, validate=True)
    except Exception:
        continue
    # 找出包含 flag{...} 的可打印部分
    print(decoded)

flag{What_1S_tHuSd4y_Quickly_VIVO50}

MISC城邦-NewKeyboard

两个流量包newkeyboard.pcapng和abcdefghijklmnopqrstuvwxyz1234567890-_!{}.pcapng，第一个为我们需要解出的usb流量，第二个为自定义的映射也是usb流量。

我们简单手动审计usb流量，发现有效的usbhid数据长度为22

用命令提取

1
2

tshark -r newkeyboard.pcapng -T fields -e usbhid.data -Y "usb.data_len == 22" > 3.txt
tshark -r "abcdefghijklmnopqrstuvwxyz1234567890-_!{}.pcapng" -T fields -e usbhid.data -Y "usb.data_len == 22" > 4.txt

写出映射程序，最后Gemni2.5Pro获胜，deepseekv3.2EXP给出了正确思路，GPT5-Thingking最拉垮了（每次给出考虑非常全面的程序，其实代码非常冗长，然后思路也不正确，思路给他了代码也写的不如另外的前面两种AI）

def solve_usb_hid_puzzle_final(mapping_file_path, target_file_path):
    """
    通过USB HID映射文件解码目标文件。
    最终修正版：精确区分“修饰键”和“字符键”数据包。

    Args:
        mapping_file_path (str): 包含按键映射数据的txt文件路径 (4.txt)。
        target_file_path (str): 需要解码的txt文件路径 (3.txt)。

    Returns:
        str: 解码后的字符串。
    """
    MAPPING_CHARS = "abcdefghijklmnopqrstuvwxyz1234567890-_!{}"
    RELEASE_PACKET = "01000000000000000000000000000000000000000000"

    def is_char_producing_packet(packet):
        """
        判断一个数据包是否会产生一个可打印的字符。
        - 它不能是“释放”包。
        - 它的普通按键码部分不能全为零。
        """
        if packet == RELEASE_PACKET:
            return False

        # 提取普通按键码部分 (从第3个字节，即第5个字符开始)
        keycode_part = packet[4:]

        # 如果按键码部分不为零，则认为是产生了字符
        return int(keycode_part, 16) != 0

    keycode_map = {}

    # 1. 建立完整且正确的映射表
    try:
        with open(mapping_file_path, 'r') as f:
            # 过滤掉所有不产生字符的数据包
            char_packets = [line.strip() for line in f if is_char_producing_packet(line.strip())]
    except FileNotFoundError:
        return f"错误：映射文件 '{mapping_file_path}' 未找到。"

    if len(char_packets) != len(MAPPING_CHARS):
        print(f"警告：识别出的字符数据包数量({len(char_packets)})与映射字符数量({len(MAPPING_CHARS)})不匹配！")

    # 将识别出的字符包与字符一一对应
    for i, packet in enumerate(char_packets):
        if i < len(MAPPING_CHARS):
            keycode_map[packet] = MAPPING_CHARS[i]

    print(f"成功建立 {len(keycode_map)} 个字符的映射。")

    # 2. 解码目标文件
    try:
        with open(target_file_path, 'r') as f:
            # 同样，只关心目标文件中产生字符的数据包
            target_char_packets = [line.strip() for line in f if is_char_producing_packet(line.strip())]
    except FileNotFoundError:
        return f"错误：目标文件 '{target_file_path}' 未找到。"

    flag = []
    for packet in target_char_packets:
        if packet in keycode_map:
            flag.append(keycode_map[packet])
        else:
            print(f"解码错误：在映射表中未找到此按键数据 -> {packet}")

    return "".join(flag)


if __name__ == '__main__':
    mapping_filename = '4.txt'
    target_filename = '3.txt'

    result = solve_usb_hid_puzzle_final(mapping_filename, target_filename)

    print("\n---------- 解码结果 ----------")
    print(result)
    print("----------------------------")

flag{th1s_is_newkeyboard_y0u_get_it!}

美妙的音乐

拖入Audacity得到flag

flag{thi5_1S_m1Di_5tEG0}

OSINT-威胁情报

在奇安信的威胁情报中心可以得到APT组织为Kimsuky

any.run平台看到EXE信息得到最早编译时间

EXE
MachineType:	Intel 386 or later, and compatibles
TimeStamp:	2021:03:31 10:23:50+00:00
ImageFileCharacteristics:	Executable, 32-bit, DLL
PEType:	PE32
LinkerVersion:	14.26
CodeSize:	232960
InitializedDataSize:	113664
UninitializedDataSize:	-
EntryPoint:	0x187fe
OSVersion:	6
ImageVersion:	-
SubsystemVersion:	6
Subsystem:	Windows GUI

也有DNS requests信息

其中alps.travelmountain.ml不在白名单内

综合所以flag为：

flag{kimsuky_alps.travelmountain.ml_2021-03-31}

日志分析-不敬者的闯入

我们在vscode打开该文件，先搜索200响应码，可以看到/admin/与webshell有关，访问/admin/可以看到下级目录存在Webshell，访问得到flag。

flag{8a9ac32b-e682-4e57-8e0e-873beda8b1cc}

Crypto

置换

给了

$ F = (1;2;3;4;5;6;7)(8;9;10;11;12;13;14) (1;3;5;7)(2;4;6)(8;10;12;14) $

计算加密置换

$ F=(14725)(36)(81112)(9101314) $

求解密置换

$ F^{−1}=(15274)(36)(81211)(9141310) $

def solve_permutation_cipher():
    """
    分析并解决基于置换的加密问题。
    """
    # 密文
    ciphertext = "SUFK_D_SJNPHA_PARNUTDTJOI_WJHH_GACJIJTAHY_IOT_STUNP_YOU."

    # 定义加密置换 F 的轮换表示
    # F = (1 4 7 2 5)(3 6)(8 11 12)(9 10 13 14)
    # 我们可以直接构建 F 的映射关系
    f_map = {}

    # 轮换 (1 4 7 2 5)
    f_map[1], f_map[4], f_map[7], f_map[2], f_map[5] = 4, 7, 2, 5, 1
    # 轮换 (3 6)
    f_map[3], f_map[6] = 6, 3
    # 轮换 (8 11 12)
    f_map[8], f_map[11], f_map[12] = 11, 12, 8
    # 轮换 (9 10 13 14)
    f_map[9], f_map[10], f_map[13], f_map[14] = 10, 13, 14, 9

    # 构建解密映射 (F 的逆)
    # 如果 F(k) = v, 那么 F_inv(v) = k
    decrypt_map = {v: k for k, v in f_map.items()}

    # 字母与数字的转换字典
    char_to_num = {chr(ord('A') + i): i + 1 for i in range(26)}
    num_to_char = {i + 1: chr(ord('A') + i) for i in range(26)}

    plaintext = ""
    for char in ciphertext:
        # 只对大写字母进行处理
        if 'A' <= char <= 'Z':
            # 字符转数字
            num = char_to_num[char]
            # 应用逆置换（解密），如果数字不在映射中则保持不变
            decrypted_num = decrypt_map.get(num, num)
            # 数字转字符
            plaintext += num_to_char[decrypted_num]
        else:
            # 非字母字符保持原样
            plaintext += char

    return plaintext


# 运行程序并打印结果
decrypted_message = solve_permutation_cipher()
print(f"解密后的明文: {decrypted_message}")

flag{SUCH_A_SIMPLE_PERMUTATION_WILL_DEFINITELY_NOT_STUMP_YOU.}

FHE: 0 and 1

此题可以利用差值和GCD来消除噪声恢复p

分析密文 c_i 的结构：
c_i = int(bit) + small_noise + large_noise
其中 bit 是我们要恢复的明文（0或1），large_noise 是 p 的倍数，small_noise 是一个小的偶数。
使用模运算简化密文：
- 对c_i进行 mod p 运算：
  c_i mod p = (int(bit) + small_noise + large_noise) mod p
- 因为 large_noise 是 p 的倍数，large_noise mod p = 0。
- 所以等式简化为：
  c_i mod p = int(bit) + small_noise
利用奇偶性恢复 bit：
- 我们知道 small_noise 永远是偶数。
- 如果 int(bit) 是 0，那么 c_i mod p = 0 + 偶数 = 偶数。
- 如果 int(bit) 是 1，那么 c_i mod p = 1 + 偶数 = 奇数。
- 因此，我们只需要检查 c_i mod p 的奇偶性，就可以100%确定bit的值。
- 遍历 ciphertext 列表中的每一个 c_i，执行此操作，拼接出完整的二进制字符串 binary_flag。

import ast
from math import gcd
from collections import Counter


def solve():
    """
    解密程序 (修正版)
    """
    # -------------------------------
    # 从文件中读取公钥和密文
    # -------------------------------
    try:
        with open("pk.txt", "r") as f:
            public_keys = ast.literal_eval(f.read())

        with open("c.txt", "r") as f:
            ciphertext = ast.literal_eval(f.read())
    except FileNotFoundError:
        print("错误：请确保 pk.txt 和 c.txt 文件在当前目录下。")
        return

    # -------------------------------
    # 步骤 1: 恢复素数 p (更稳健的方法)
    # -------------------------------
    print("[*] 正在使用更稳健的方法恢复素数 p...")

    # 1. 计算公钥两两之间的差值 (取一个适中的样本量以提高效率)
    # 如果 public_keys 列表过长，全部计算差值会很慢，所以我们只取前 200 个密钥来计算。
    num_keys_for_p_recovery = min(200, len(public_keys))
    diffs = [abs(public_keys[i] - public_keys[j])
             for i in range(num_keys_for_p_recovery)
             for j in range(i + 1, num_keys_for_p_recovery)]

    # 2. 计算这些差值之间的两两最大公约数
    # 这样可以有效地消除随机偏移量带来的“噪声”
    gcds = []
    # 为了效率，我们只取一部分差值进行两两组合
    num_diffs_to_use = min(100, len(diffs))
    for i in range(num_diffs_to_use - 1):
        for j in range(i + 1, num_diffs_to_use):
            g = gcd(diffs[i], diffs[j])
            # p 是一个128位的大素数，所以我们只关心那些足够大的GCD结果
            if g.bit_length() > 100:
                gcds.append(g)

    # 3. 找到出现次数最多的GCD，这极有可能就是 p
    if not gcds:
        print("[!] 错误：未能找到任何可能的大素数公约数。")
        print("[!] 可能的原因是用于计算的密钥样本量太小或数据有问题。")
        return

    # 使用 Counter 统计每个大GCD出现的次数
    p_candidate, count = Counter(gcds).most_common(1)[0]
    p = p_candidate

    print(f"[*] 成功恢复素数 p: {p}")
    print(f"[*] p 的位长度: {p.bit_length()}")

    # 基本的验证，p 应该是 128 位
    if p.bit_length() < 120 or p.bit_length() > 130:
        print("[!] 警告：恢复的 p 位数不符合预期 (128位)，解密结果可能不正确。")

    # -------------------------------
    # 步骤 2: 解密密文
    # -------------------------------
    binary_flag = ""
    for c_i in ciphertext:
        remainder = c_i % p
        if remainder % 2 == 1:
            binary_flag += "1"
        else:
            binary_flag += "0"

    print(f"\n[*] 恢复的二进制 Flag: {binary_flag[:64]}...")

    # -------------------------------
    # 步骤 3: 将二进制转换为 ASCII
    # -------------------------------
    flag = ""
    try:
        for i in range(0, len(binary_flag), 8):
            byte_str = binary_flag[i:i + 8]
            if len(byte_str) < 8: continue  # 忽略末尾不足8位的部分

            char_code = int(byte_str, 2)
            flag += chr(char_code)
    except (ValueError, TypeError) as e:
        print(f"\n[!] 在将二进制转换为 ASCII 时出错: {e}")
        print("[!] 可能的原因是恢复的素数 p 不正确。")
        return

    print(f"\n[+] 成功解密 Flag: {flag}")


if __name__ == "__main__":
    solve()

flag{3235c1ab-6830-480f-b5e0-39be40b94a7d}

RSA_revenge

题目

# 这段脚本把 flag 拆成两半并分别加密

from Crypto.Util.number import *
import random


# 原始 flag
flag = b'flag{???????????????????}'
length = len(flag)

# 把 flag 分成前后两半，分别转换为整数 m1, m2
m1 = bytes_to_long(flag[:length//2])
m2 = bytes_to_long(flag[length//2:])

# ------------------------- par1: 构造第1类模 n1 并加密 m -------------------------
def par1(m):

    lst = []
    # 选取 3 个不同的大素数（每个 512 bit）
    while len(lst) < 3:
        prime = getPrime(512)
        if prime not in lst:
            lst.append(prime)
            print(prime)

    # n1 = ∏ p_i^{t_i}，其中每个素因子 p_i 被随机提升到 2到7 的小幂
    n1 = 1
    for prime in lst:
        tmp = random.randint(2, 7)   # 指数 tmp 在 2到7 之间
        print(tmp)
        n1 *= prime ** tmp

    e = 65537
    # 在模 n1 下对 m 做 RSA 加密
    c1 = pow(m, e, n1)

    # 输出素因子列表、模 n1、密文 c1

    print(f"list：{lst}")
    print(f"n1={n1}")
    print(f"c1={c1}")


# ------------------------- par2: 构造第2类模 n2 并加密 m，给出多个 hint -------------------------
def par2(m):

    # 随机选三个不同的大素数 p2,q2,r2（每个 512 bit），并把它们相乘得到 n2
    while True:
        p2 = getPrime(512)
        q2 = getPrime(512)
        r2 = getPrime(512)
        if p2 != q2 and p2 != r2 and q2 != r2:
            break

    n2 = p2 * q2 * r2


    hint1 = pow(m, p2 * q2, n2)
    hint2 = pow(m, r2, n2)        # 怎么用好 hint1 和 hint2 呢？试一试 Fermat 吧！
    hint3 = p2 + q2               # hint3 很关键 —— 想想如果你知道 p+q 和 p*q，就能做什么？

    e = 65537
    c2 = pow(m, e, n2)

    print(f"n2={n2}")
    print(f"hint1={hint1}")
    print(f"hint2={hint2}")
    print(f"hint3={hint3}")
    print(f"c2={c2}")

# 分别运行两部分，对 flag 的前半段/后半段加密并输出相关提示
par1(m1)
par2(m2)

第一部分，n1的素因子已知，但指数不知，指数可以用n2逐个除素因子试出，然后求欧拉函数，常规的RSA了

第二部分，考查费马小定理或者说是同余的性质

\[ hint_2\equiv m^{r_2} \pmod {n_2} \\ \Rightarrow hint_2 \equiv m^{r_2} \pmod {r_2} \equiv m \pmod{r_2} \]

\[ c_2 \equiv m^e \pmod{n_2} \\ \Rightarrow c_2 \equiv m^e\pmod{r_2} \]

所以有

\[ c_2 \equiv hint_2^e\pmod{r_2} \\ \Rightarrow c_2 = hint_2^e + kr_2 \]

\[ r_2 = gcd(hint_2^e-c_2,n_2) \]

得到r2后就知道p*q了，进而求出phi2，然后就是常规RSA了

from gmpy2 import *
from Crypto.Util.number import *
n2 = 1069018081462192233874980694931144545150390355151142000407896565228521856087497130221328822828336193888433906258622424173888905902703892967253752403237818439004204769185744957222426788163474091322195131517000927031632213563726678357776820914860304114493023487392954636569155416533134778017635963554249754152905136768251720862406591818283210776943594065154793598910172412634428403766286774221252340847853800584819732893065160890727141088203583945705491817754798199
hint2 = 30328561797365977072611520167046226865857127358764834983211668172910299946455309984910564878419440651867811045905957544019080032899770755776597512870488988655573901143704158135658656276142062054235425241921334990614594054774876139797881802290465401101513930547809082303438739954539239681192173563314964619128522116071538744700209974655230351192503911493028021717763873423132332205605117704777006410273001461242351682504368760936763922017247768057874236213463076
hint3 = 20884722618082876001516601155402590958389763080024067634953470674302186115943562475648388511118550021010685094074280890845364756164094187193286427464829840
c2 = 548415661734126053738347374438337003873176731288953351164055019598761821990636552806558989407452529293973596759395078164177029251755832478675308995116633955485067347066419466003081030015784908106772410713523387155248930421498438336128348929737424937920603679054765413736671822930257854740643178209639013528748572597042833138551717910328899462934527011212318128877188460373648545379405946354668400634037669394938860103705689139981117990256660685216959315741336968
e = 65537
p1_list = [8477643094111283590583082266686584577185935117516882965276775894970480047703089419434737653896662067140380478042001964249802246254766775288215827674566239,
           7910991244809724334133464066916251012653855854025088993280923310153569870514093484293150987057836939645880428872351249598065661847436809250099607617398229,
           12868663117540247120940164330605349884925779832327002530579867223566756253418944553917676755694242046142851695033487706750006566539584075228562544644953317]
n1 = 1103351600126529748374237534378639752005563260397057273760573608668234841858898339963615180586483636658319719258259564340229731088477043006707066258091746453519875771328756343070392346553837475869985292233339882321767365588480914243055530194543710833400735694644740966837509139443272712871728933520755003149497543272631963356726446399042360341133139923381402765176034620742095462597690819317740258280338778466308360122325510768573457366480478480385099879072314101166576014811788437611871531848011762293407180575205681864374034973560073644731757180275405672624629974899658185645498677923049149478738083257882839079796420483489134608949730373829870700049152830490730902518823469250714236113622490232617166274965015245948264281265453208875232918994116540222173029738472689551464384951129495828658025526216028826258099588572669439254177489891457890498930044291769038333452721765661715836795838845421437984152253836745540547878024331492328801233425013069672422548913381714868180440419922587534373534388179645778998201569812711853469607955639409976100938326204393436455902117700715705355730254907473694496862186927081288536664564066273905636691443629865742113665395817897790346568115147261785693069547062993147965228097215778787698574672103567611954541526351385121096946876318405181900957517179318858167322380305506577864659070587276190351263272904670121000123739762817165611376508091511049581310489960967300251226150505529874043827860587179066433478573304632672443028389332137578559069790875583860034559992961597964011009181097461053565357444468759142467793785272517357594961007684369171923169825343428400994582000709315829746271356743493827706669902956302087422710335869361908872578360718630332916867987882367454381486160119341248986730614715669587555561672656107579415221691270769054441036888212622679174466809685017295395823904506545225068526453243179279430769878809345179954207934650512040934969514434321887565917951423932360150276928683390148666338790317001765138293050858448249492058987889761085236104153306884365020403974305552987123976314900738336243171779096705121428628914344115125836293982077268043357822313817090167616525512714228298048543723340688062975654817272989686281447834032081689520522343318726816659742944874587243087717935463623631288732784108299093601104113561688659145661286269339180833210463
c1 = 1091994761217634826072124019708574984391652131019528859451478177360336520455071879664626056517127684886792263267184750289726966173475531785135908239241367011964947254146686336678625127107000203921535502636024125382397949549706019108806905113568387688784083651867765356465676713044867529224095280990952281722377729904633765755308727317586804384907594623294542255582608130775388385053656500091188492219892541287152759373311871679053567569991598739628072091647402994694057021522875429987401797108991466209720726320411739418901734326490258573985380323870664455719118307333460877640654186421881374126846465164012283741829305792336376443671697322944983680753186871994926812712407530175535547953488409667363778877011722921746615125168842335755090712330314248078688305813574126414154357295682111730319771541764882123530538798904329448342477283010679916534388272354852606444335501019923314748714020060783702757991765107811664795881473290112012642711848840732656792842975595985262637352884148989392358729413049666423809444629233355604344713121576947744271550672311509709353155584615401385981281541568915650140285513857950097872392262841978506457072907666348887936981254691271750737368646952613446340505887570613771043863966115924851279285010321193299940403084752305457659188900451883509679442577291500194294702408740417770241347854055121038455584689346661759142226424655750649030196509606345959868857460928822458178193914427975718432613693148519385509070885413086890691471063639321214058351800789483569828355240522324245612035847073723555128381268497293297681153943700076717509367055194706714770699658667364019792069384855913700111098207862666478388154325649690787295929427544059466206456378068191323286585251490682952650730101051661446454500997013269750318207079005140046631065420740924251847948208391204635801689730778074655515676216581230345037704163062457051532737078339281175699645868527505281984564077081473213204937490995858702477009964928872064904754834804222961572810639265783286770899262602346777948115933216112376126550352514674411338374863486761612733848198090788549337632188615953986569772932102409611086086895003705261003974939487286850347660140334361903821934552381535024019082394626749532280515222512480387681995937963724398131252527927016338174692268363933916957519992512787514236065140642709723084266949
nn = n1
exponents = []
for p in p1_list:
    exp = 0
    while nn % p == 0:
        exp += 1
        nn //= p
    exponents.append(exp)
print("Exponents:", exponents)

phi1 = 1
for p, exp in zip(p1_list, exponents):
    phi1 *= (p ** (exp - 1)) * (p - 1)

d1 = pow(e, -1, phi1)
m1 = pow(c1, d1, n1)
m1_flag=long_to_bytes(m1)
r2 = gmpy2.gcd(pow(hint2,e,n2)-c2,n2)
pq2 = n2//r2
phi2 = (pq2-hint3+1)*(r2-1)
d2 = inverse(e,phi2)
m2_flag = long_to_bytes(pow(c2,d2,n2))
print(m1_flag+m2_flag)

flag{Ooooo6_y0u_kn0w_F3rm@t_and_Eu13r_v3ry_w3ll!!}

群论小测试

通过分析群的 Cayley 乘法表来识别具体的群类型。挑战需要连续正确识别 5 个群才能获得 flag。

1. 循环群 (Cyclic Groups)

特征: 阿贝尔群，存在 n 阶生成元
识别: 检查是否存在元素阶数等于群阶数

2. Klein 四元群 (V4)

特征: 4阶阿贝尔群，所有非单位元都是2阶
识别: 4阶群，阿贝尔，没有4阶元素

3. 对称群 S3

特征: 6阶非阿贝尔群
识别: 6阶，非阿贝尔

4. 二面体群 D4, D5, D6

特征: 非阿贝尔，D4有5个2阶元素
识别: 检查2阶元素数量

5. 四元数群 Q8

特征: 8阶非阿贝尔群，只有1个2阶元素
识别: 与D4区分的关键是2阶元素数量

6. 交错群 A4, A5

特征: A4有8个3阶元素
识别: 统计3阶元素数量

from pwn import *
import re
from sage.all import *

def parse_cayley_table(table_text, n):
    """解析Cayley表文本"""
    lines = table_text.strip().split('\n')
    table_data = []
    
    for line in lines:
        # 跳过分隔线和空行
        if not line.strip() or line.startswith('-'):
            continue
        
        # 解析数据行 - 行号 + n个数据
        parts = line.split()
        if len(parts) >= n + 1:  # 行号 + n个数据
            try:
                # 第一个元素是行号，后面的n个元素是表格数据
                row_data = [int(x) for x in parts[1:1+n]]
                if len(row_data) == n:
                    table_data.append(row_data)
            except ValueError:
                continue
    
    # 确保我们有n行数据
    if len(table_data) == n:
        return table_data
    else:
        print(f"警告: 期望{n}行数据，但只解析出{len(table_data)}行")
        return table_data

def check_abelian(table):
    """检查群是否阿贝尔"""
    n = len(table)
    for i in range(n):
        for j in range(n):
            if table[i][j] != table[j][i]:
                return False
    return True

def find_identity(table):
    """找出单位元"""
    n = len(table)
    for candidate in range(n):
        is_identity = True
        for i in range(n):
            if table[candidate][i] != i or table[i][candidate] != i:
                is_identity = False
                break
        if is_identity:
            return candidate
    return None

def calculate_orders(table, identity):
    """计算每个元素的阶"""
    n = len(table)
    orders = []
    
    for element in range(n):
        if identity is None:
            # 如果没有找到单位元，使用简单方法
            orders.append(1)
            continue
            
        order = 1
        current = element
        while current != identity and order <= n:
            current = table[current][element]
            order += 1
        orders.append(order)
    
    return orders

def identify_group(table):
    """识别群的类型"""
    n = len(table)
    is_abelian = check_abelian(table)
    identity = find_identity(table)
    
    if identity is None:
        print("警告: 未找到单位元，使用默认识别")
        if is_abelian:
            return f"C{n}"
        else:
            if n == 6:
                return "S3"
            elif n == 8:
                return "D4"  # 默认猜D4
            else:
                return f"D{n//2}"
    
    orders = calculate_orders(table, identity)
    
    # 统计各阶元素数量
    order_counts = {}
    for order in orders:
        order_counts[order] = order_counts.get(order, 0) + 1
    
    print(f"群阶数: {n}")
    print(f"阿贝尔: {is_abelian}")
    print(f"单位元: {identity}")
    print(f"元素阶数分布: {order_counts}")
    
    # 根据阶数和性质识别群
    if n == 1:
        return "C1"
    elif n == 2:
        return "C2"
    elif n == 3:
        return "C3"
    elif n == 4:
        if is_abelian:
            # 检查是否有4阶元素
            has_order4 = any(order == 4 for order in orders)
            return "C4" if has_order4 else "V4"
        else:
            return "S3"
    elif n == 5:
        return "C5"
    elif n == 6:
        if is_abelian:
            return "C6"
        else:
            return "S3"
    elif n == 7:
        return "C7"
    elif n == 8:
        if is_abelian:
            return "C8"
        else:
            # D4有5个2阶元素，Q8有1个2阶元素
            order2_count = sum(1 for order in orders if order == 2)
            return "D4" if order2_count == 5 else "Q8"
    elif n == 9:
        return "C9"
    elif n == 10:
        if is_abelian:
            return "C10"
        else:
            return "D5"
    elif n == 12:
        if is_abelian:
            return "C12"
        else:
            # A4有8个3阶元素
            order3_count = sum(1 for order in orders if order == 3)
            return "A4" if order3_count == 8 else "D6"
    elif n == 24:
        return "S4"
    elif n == 60:
        return "A5"
    elif n == 120:
        return "S5"
    else:
        # 默认情况
        if is_abelian:
            return f"C{n}"
        else:
            return f"D{n//2}"

def solve_challenge():
    """主解题函数"""
    conn = remote('47.94.87.199', 20769)
    
    rounds_completed = 0
    max_rounds = 5
    
    try:
        buffer = b""
        while rounds_completed < max_rounds:
            # 持续接收数据
            chunk = conn.recv(1024, timeout=2)
            buffer += chunk
            text = chunk.decode('utf-8', errors='ignore')
            print(text, end='')
            
            # 检查是否到了输入提示
            if b"Your answer" in buffer:
                full_output = buffer.decode('utf-8', errors='ignore')
                
                # 提取阶数n
                n_match = re.search(r'order n=(\d+)', full_output)
                if n_match:
                    n = int(n_match.group(1))
                    print(f"检测到群阶数: {n}")
                    
                    # 提取表格部分
                    table_start = full_output.find("  0")
                    if table_start == -1:
                        table_start = full_output.find("   0")
                    
                    if table_start != -1:
                        table_end = full_output.find("Your answer", table_start)
                        if table_end != -1:
                            table_text = full_output[table_start:table_end].strip()
                            
                            print("提取到的表格:")
                            print(table_text)
                            
                            # 解析表格
                            table_data = parse_cayley_table(table_text, n)
                            if table_data and len(table_data) == n:
                                print(f"成功解析表格，大小: {len(table_data)}x{len(table_data[0])}")
                                
                                # 识别群类型
                                group_type = identify_group(table_data)
                                print(f"识别出的群类型: {group_type}")
                                
                                # 发送答案
                                conn.sendline(group_type.encode())
                                
                                # 读取响应
                                try:
                                    response = conn.recvuntil(b'\n', timeout=2)
                                    response_text = response.decode('utf-8', errors='ignore')
                                    print(response_text)
                                    
                                    if "Correct" in response_text or "Progress" in response_text:
                                        rounds_completed += 1
                                        print(f"进度: {rounds_completed}/{max_rounds}")
                                except:
                                    print("读取响应超时")
                                
                                # 重置缓冲区
                                buffer = b""
                            else:
                                print(f"表格解析失败，期望{n}行，实际{len(table_data) if table_data else 0}行")
                                # 发送默认答案
                                if n == 8:
                                    conn.sendline(b"D4")
                                elif n == 6:
                                    conn.sendline(b"S3")
                                else:
                                    conn.sendline(b"C" + str(n).encode())
                        else:
                            print("未找到表格结束位置")
                    else:
                        print("未找到表格开始位置")
                        # 发送默认答案
                        if n == 8:
                            conn.sendline(b"D4")
                        elif n == 6:
                            conn.sendline(b"S3")
                        else:
                            conn.sendline(b"C" + str(n).encode())
                
                # 重置缓冲区等待下一轮
                buffer = b""
        
        # 读取flag
        print("等待flag...")
        flag_data = conn.recvall(timeout=5)
        print("最终输出:")
        print(flag_data.decode('utf-8', errors='ignore'))
        
    except Exception as e:
        print(f"发生错误: {e}")
        import traceback
        traceback.print_exc()
    
    finally:
        conn.close()

if __name__ == "__main__":
    solve_challenge()

flag{I_v3_b3c0m3_@n_e^3Rt_in_gr0up_7h30ry_@Ft3r_5o1ving_7hi5_+++bl3m!!!}

DLP_1

之前刷博客刷到的，sage中另一种求离散对数的方法

from Crypto.Util.number import long_to_bytes
p=[189869646048037, 255751809593851, 216690843046819]
g=[5, 3, 3]
h=[78860859934701, 89478248978180, 81479747246082]
flag = b""
for i in range(3):
    part = int(pari(f"znlog({int(h[i])},Mod({int(g[i])},{int(p[i])}))"))
    flag += long_to_bytes(part)
print(b'flag{'+flag+b'}')

flag{I_l0v3_DLPPPPP^.!}

6jf's blog

NewStarCTF2025_week1&2

Week1

Misc

我不要革命失败

MISC城邦-压缩术

EZ_fence

前有文字，所以搜索很有用

OSINT-天空belong

Crypto

唯一表示

小跳蛙

初识RSA

随机数之旅1

Sagemath使用指哪？

Week2

Misc

星期四的狂想

MISC城邦-NewKeyboard

美妙的音乐

OSINT-威胁情报

日志分析-不敬者的闯入

Crypto

置换

FHE: 0 and 1

RSA_revenge

群论小测试

1. 循环群 (Cyclic Groups)

2. Klein 四元群 (V4)

3. 对称群 S3

4. 二面体群 D4, D5, D6

5. 四元数群 Q8

6. 交错群 A4, A5

DLP_1

Week1

Misc

我不要革命失败

MISC城邦-压缩术

EZ_fence

前有文字，所以搜索很有用

OSINT-天空belong

Sign in

Crypto

唯一表示

小跳蛙

初识RSA

随机数之旅1

Sagemath使用指哪？

Week2

Misc

星期四的狂想

MISC城邦-NewKeyboard

美妙的音乐

OSINT-威胁情报

日志分析-不敬者的闯入

Crypto

置换

FHE: 0 and 1

RSA_revenge

群论小测试

1. 循环群 (Cyclic Groups)

2. Klein 四元群 (V4)

3. 对称群 S3

4. 二面体群 D4, D5, D6

5. 四元数群 Q8

6. 交错群 A4, A5

DLP_1